【学习笔记】生成模型——能量视角下的生成对抗网络
先说说我为什么会想研究Energy Based Model吧。之前我写过一套笔记介绍一系列的GANs,其中有一个模型叫做EBGAN,它最有特色的地方是它的判别器,长成下面这个样子:

当时在介绍这个判别器的作用时,是说“其不再去鉴别输入图像是来自于![]() 还是
还是![]() ,而是去鉴别输入图像的重构性高不高”。更详细点解释就是,图中Autoencoder是一个提前用真实样本训练好的网络,现在要鉴别一个输入图像是真还是假,只需把这张图放入Autoencoder中,如果它是真实图片的话通过此Autoencoder重构回的图像就基本是无损的(因为这个Autoencoder就是用真实样本训练出来的),而如果是假造图片的话重构图像就会与原图差别较大,因此这个Autoencoder输出和输入图片的差异就能够作为这个判别器的打分值。
,而是去鉴别输入图像的重构性高不高”。更详细点解释就是,图中Autoencoder是一个提前用真实样本训练好的网络,现在要鉴别一个输入图像是真还是假,只需把这张图放入Autoencoder中,如果它是真实图片的话通过此Autoencoder重构回的图像就基本是无损的(因为这个Autoencoder就是用真实样本训练出来的),而如果是假造图片的话重构图像就会与原图差别较大,因此这个Autoencoder输出和输入图片的差异就能够作为这个判别器的打分值。
其实上述的这种判别器,如果细细一想的话,会让人觉得非常奇怪,因为它不符合我们在理论上对于GANs的认知:判别器的根本目的是要计算两个分布之间的散度(Divergence),从而为生成器提供梯度的正确引导。但是在上述的这个判别器中,它只用到了真实样本去训练,训练结果是无法计算出任何两个分布间的散度的,那么它该如何为生成器提供正确的引导呢?这样的EBGAN究竟是如何起作用的呢?
带着困惑我去阅读了原paper和很多相关笔记,然后神奇地发现,我们原有对于GANs的认知没有错误但不充分,那是一种基于PBM(Possibility Based Model)的认知方法,但是其实对于GANs的认知还有另外一个维度,那就是把GANs视作一种EBM(Energy Based Model)模型。
下面先简要介绍一下这两种思维方法的差异。
1.PBM与EBM的比较

基于概率模型(PBM)的GANs
首先将GANs视作一种PBM,也就是基于概率的模型,这是被大众普遍接受的认知方法,因为熟悉GANs理论的朋友会知道,判别器的本质是计算样本x属于类别y的条件概率P(y|x)(其中y只有正负两类所以判别器就是一个二分类器),生成器的本质是计算样本x在整个分布中的生成概率,也就是联合概率P(xy)。那么概率的计算,需要基于样本的统计才能实现,这意味每一个样本都需要有明确的正/负维度,也就是喂给判别器的输入非负即正(正指真实样本,负指生成样本),无它。只有这样,判别器才能基于概率正确计算出正负样本分布间的散度(Divergence),进而帮助生成器产生更逼近正样本的负样本出来。

基于能量模型(EBM)的GANs
但是对于EBM,也就是基于能量的模型而言,它就不需要所有样本都具有明确的正/负维度了。因为它用一种更灵活的、称之为“能量”的东西去代替了概率计算。

能量的含义很抽象,我们不妨用一个能量函数U(x)去衡量它,正样本本身具有最低的能量函数,样本越远离正样本能量值就越高。并且能量具有吸引力,也就是能量值低的样本会吸引能量值高的样本向自己靠近。后文会对能量模型有更清晰的介绍。
现在不妨比较一下两种模型的异同。在GANs视角下,二者都具有生成器与判别器,但是对于PBM模型而言生成器是核心,而对于EBM模型而言判别器是核心。这是因为,在PBM理论中,一开始只设计了生成器,没有判别器,但是因为生成器的计算中缺失正负样本间的散度,不得已再构造了一个判别器去学习计算这个散度,进而辅助生成器;而在EBM理论中,一开始只构造了判别器,没有生成器,但是因为判别器的计算中缺失负样本,不得已再构造了一个生成器去学习提供负样本,进而辅助判别器。后文会有关于EBM理论的更详细的介绍。
另外,从宏观上来看,PBM比较依赖于正样本和负样本,而EBM可以不依赖于负样本。换言之,PBM中的判别器就好比是一根吸管,它需要明确知道正、负样本的接口在哪,才能帮助生成器顺着这根吸管将负样本朝正样本靠近;但是EBM中的判别器就好比是一块磁铁,只需把它安置在正样本上,就能借用能量的优势将周围的负样本吸引向自身。
2.EBM的设计思维
在这一节我们将会介绍能量模型到底是一种什么模型,首先我们需要解释能量是什么。能量本身这个词是来自于物理学中的一个数学概念,能量模型是AI大牛Yann LeCun于2006年发表的论文《A Tutorial on Energy-Based Learning》中提出的方法,这篇paper长达59页,可想而知能量模型是一种多么复杂的模型。那在本文中为了更通俗地讲解,我们摒弃掉复杂繁晦的数学建模,借用苏剑林老师在PaperWeekly中撰写的专文《能量视角下的GAN模型》,我们用更直白有趣的方法来理解能量模型。
能量的概念,可以理解为“坑”,而能量模型下的GANs,就是一个不断“挖坑”与“跳坑”的过程。

一开始,能量函数只是一条平直的直线。
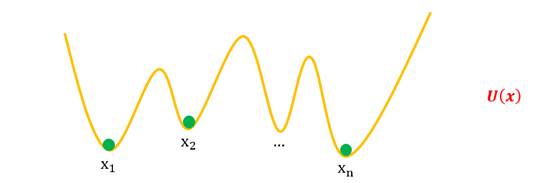
然后将真样本 ![]() ,压出一条凹凸不平的函数,将其固定住,
,压出一条凹凸不平的函数,将其固定住,![]() 就构成了一个能量函数。
就构成了一个能量函数。

接下来我们得到一批生成样本,![]() ,将它们任意放置于
,将它们任意放置于![]() 上。然后固定住U(x),松开
上。然后固定住U(x),松开![]() ,于是
,于是![]() 就会顺着“能量”的坡度慢慢滚落到坑底,而坑底代表着真实样本,所以
就会顺着“能量”的坡度慢慢滚落到坑底,而坑底代表着真实样本,所以![]() 都变得很像真样本了。
都变得很像真样本了。
上述就是在能量视角下GANs训练过程的最简单的展示。
我们可以基于这一设想开始初步数学建模。
首先考虑判别器——“挖坑”的过程。我们希望真样本能放到“坑底”,假样本能放到“坑腰”,这意味着假样本的“平均海拔”要高于真样本的“平均海拔”,也就是说:
![]()
尽量小,这里我们用 p(x) 表示真实样本的分布,q(x) 表示假样本的分布。假样本通过 x = G(z) 生成,而z来自 z∼q(z) 是标准正态分布。
进一步,我们还希望真样本要在坑底,用数学的话说,坑底就是一个极小值点,导数等于 0 才好,即要满足![]() 是最理想的,换成优化目标的话,那就是
是最理想的,换成优化目标的话,那就是![]() 越小越好。两者综合起来,我们就得到 U 的优化目标:
越小越好。两者综合起来,我们就得到 U 的优化目标:

值得说明的是,上述的U(x)函数在实际训练中一定是要做限制处理的,否则神经网络可以将U(x)(x~p(x))无限拉低,U(x)(x~q(x))无限拔高,这样模型就永远不会收敛。对应的解决方法可以参考WGAN中的梯度裁剪,WGAN-GP中的梯度惩罚,以及SNGAN中的lipschitsz限制,这些都在GANs介绍系列文章中有详细说明,在此就不细述。
接下来我们可以构建生成器——“跳坑”的过程。此时坑挖好了, U(x)固定了,我们让假样本滚到坑底,也就是让 U(x) 下降,滚到最近的一个坑,所以:
![]()
至此,我们就完成了“填坑模型”的初步建模过程。但是,真实情况的“坑”并非都像上面的图那么简单,因为“坑的模型”本身就会有很多坑,我们需要格外小心才行。

比如,上图中假样本![]() 慢慢下滑,并不一定能到达 x1 的坑,而是到达一个中间的坑,这个中间的坑并非代表真样本,可能仅仅是“次真”的样本,所以我们需要不断地改进假样本,也需要不断地把坑修正过来(比如争取能下一步把阻碍前进的峰“削掉”)。
慢慢下滑,并不一定能到达 x1 的坑,而是到达一个中间的坑,这个中间的坑并非代表真样本,可能仅仅是“次真”的样本,所以我们需要不断地改进假样本,也需要不断地把坑修正过来(比如争取能下一步把阻碍前进的峰“削掉”)。
我们也可以考虑在优化的时候添加动量,如下图所示:
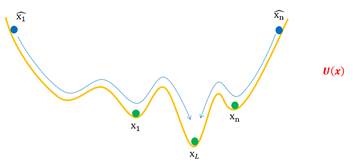
但是这样也会导致新的问题:有的假样本越过最近的坑,到达更远的坑去,导致假样本聚集在某些真样本附近,进而出现Mode Collapse(样本多样性丧失)问题。
另外,生成样本的初始分布也是一个容易导致多样性丧失的因素,如下图所示,当初始的假样本同时聚在个别坑附近时,同样会产生Mode Collapse。
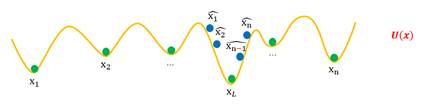
由此可以看出,目前我们构建的“坑的模型”,最大的一个隐患就是容易导致Mode Collapse。简单来看,Mode Collapse 是因为假样本们太集中,不够“均匀”,所以我们可以往生成器中加一个损失项,让假样本有均匀的趋势。这个项就是假样本的熵 H(X)=H(G(Z)),我们希望假样本的熵越大越好,这意味着越混乱、越均匀,所以生成器的目标可以改为:
![]()
接下来我们需要做的,就是找到这个H(x)函数,这将会需要一些严密的数学推导。我们先在第三节构建更完备的理论基础,然后再在第四节求解H(x)。
3.EBM的理论分析
回到最开始生成模型在探讨的问题上:我们有一批数据 x1, x2, … , xn ∼ p(x),我们希望用一个概率模型去拟合这批数据的分布。
我们选取一种这样的模型:

其中Uθ 是带参数 θ 的未定函数(即能量函数),而 Zθ 是归一化因子(即配分函数),Zθ的表达式为:
![]()
上式就是能量模型中最核心的表达式,但是,一定会有不少人困惑,这式子到底是如何得到的?下面就将提出三点问题,并一一解答。
第一个问题,为何能够选用这样的式子?首先来看一下大体规律,如果x属于真实图片,那么Uθ(x)的值是最低的,也就是样本的概率值qθ(x)的值是最高的;而如果x不属于真实图片,离真样本越远Uθ(x)就越高,也就是样本的概率值qθ(x)会越低。因此能量函数qθ(x)是符合真实样本p(x)的分布规律的,在调整参数θ的情况下让qθ(x)完全逼近p(x)是可能做到的。另外,如果将-Uθ(x)看作是通用的神经网络的表达式的话,qθ(x)就相当于加了一个Softmax层。
第二个问题,这个式子是如何被构造出来的?大致引述一下:
MCMC(Markov Chain Monte Carlo)告诉我们,我们难以直接从某个给定的分布 q(x) 中采样出样本来,但是我们可以构造如下的随机过程:
![]()
其中 α 是一个便于实现的随机过程,比如从二元分布、正态分布采样等。
当我们取f为Langevin 方程时,这一随机过程就变成了:
![]()
而对于Langevin 方程,当 ε→0 时,它的静态分布就正好是能量分布:
![]()
所以,原有表达式其实来自一种特定的随机过程在ε→0下的分布表达式。
第三个问题,选用这样的模型表达式优势在哪?简单来说,对这个式子求导并且取期望的结果,就刚好能拆分成真实分布与拟合分布的均值之差,进而能构造GANs网络。下面我们就会逐步解读如何应用这一能量模型去构建GANs网络。
现在我们已完成了建模,接下来需要求解参数θ。
将qθ(x)取对数后,目标函数定义为:
![]()
我们希望它越大越好,也就是希望下式越小越好:
![]()
为此,我们对 Lθ 使用梯度下降。由于:

所以(第二项对于Ex~p(x)是常数,所以可以省略掉外边的Ex~p(x)):
![]()
不妨观察一下这个式子的特点,它是分别在真实分布下和拟合分布下的均值之差,可以看作是对原始表达式作了“正相”和“负相”的分解,这是与GANs的思维很接近的部分。
把上式代入到梯度下降的更新公式中,得到:
![]()
至此我们就在理论上初步完成了对于能量模型的建模和求解,似乎是很容易就推导出来了。我们不妨尝试着把这一套公式放在神经网络(称之为判别网络)中去训练。
不过,很快我们就发现了问题,上述公式中的第二项,即满足qθ(x)的x的采样是缺失的。因为qθ(x)非常地复杂,所以试图人为地采样是不可取的,于是我们只好考虑,是否能再构造出一个神经网络(称之为生成网络),能够专门用来提供满足qθ(x)的样本。
对于这个生成网络,我们记输入为z,输出为x,且满足:
![]()
这里的 q(z) 代表着标准正态分布。也就是说,我们可以从标准正态分布中采样出一个 z 出来,然后通过固定的模型 Gφ 变换为我们想要的 x,通过这种方式得到的数据分布可以表示为:
![]()
下面我们要做的就是让生成数据分布qφ(x)逼近qθ(x),用KL散度去衡量qφ(x)与qθ(x)之间的相似性,表达式如下:

其中![]() ,代表 qφ(x) 的熵。
,代表 qφ(x) 的熵。
我们希望qφ(x)与qθ(x)之间的KL散度值最小,也就是求解出参数φ,使得:
![]()
这一式子便是生成网络的损失函数,值得注意的是,在这个表达式中,-Hφ(X) 希望熵越大越好,这意味着多样性;![]() 希望图片势能越小越好,这意味着真实性。也就是说,φ对应的生成网络能够有效避免Mode Collapse问题,即生成样本是可靠的。
希望图片势能越小越好,这意味着真实性。也就是说,φ对应的生成网络能够有效避免Mode Collapse问题,即生成样本是可靠的。
另外,回顾之前第二节最后提出的那个问题——待求解的熵H(x),也就对应到了上式理论推导中的Hφ(X),而目前一堆理论推导下来,我们得到的结论是,如果我们构建一个生成网络去拟合生成样本的话,在用KL散度作损失函数的情况下,我们得到的生成样本是能够实现熵高的需求,也就是能解决当初在构思能量模型时对于Mode Collapse的担忧。
不过,φ的表达式还不足以构造完整的神经网络,因为只有第二项是分布的期望表达式,第一项Hφ(X)还需要进一步变形求解。由于Hφ(X)的求解比较复杂,这一过程将会被单独放在第四节介绍。现在不妨假设现在Hφ(X)已经求解出了,因为这样能比较快地完成整套能量模型的理论推导。
假设φ的完整表达式已知,即生成网络能提供缺失样本(x~qθ(x))了。下面只需把这个生成网络代入到原判别网络中去,也就是判别网络的更新公式变更为:
![]()
替换成θ的目标表达式就是:
![]()
考虑到第二节当中提及的“真样本要在坑底”的限制,我们可以给θ再添加一个惩罚项。于是最终两个网络的训练表达式为:

上述便是在能量模型下GANs的完整理论推导。
我们简要地做一个梳理,EBGAN最开始从判别网络的角度出发,构建了一个能量模型希望能够拟合真实数据,但是在推导的过程中发现来自“负相”的样本是缺失的,于是又引入了生成网络希望能学会提供“负相”样本。在搭建生成网络时采用了一种容易采样的模型,于是困难的地方在于如何让生成样本逼近“负相”样本(第四节会解决)。解决好后,便能将生成网络代入到原判别网络,二者交替训练就构成了一个完整的GANs模型。
4.* Hφ(X)的求解
这一节我们要求解的式子如下:
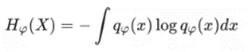
代表 qφ(x) 的熵,而 qφ(x) 的理论表达式是:
![]()
由此可以看出,Hφ(X) 由于嵌套了积分,想直接计算是非常困难的。我们可以考虑将熵的计算转化为其他的计算,譬如互信息Iφ(x,z)(一种衡量两个东西相关性的指标)。
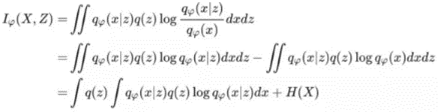
在上式中可以看出,我们找到了X,Z的互信息与X的熵之间的关系,它们的差是:
![]()
事实上 Hφ(X|Z) 称为“条件熵”。
现在我们考虑,求解熵是否能转化成求解互信息相关的东西。
如果我们处理的是离散型分布,那么因为 x=Gφ(z) 是确定性的,所以 qφ(x|z)≡1,那么 Hφ(X|Z) 为 0,即 Iφ(X,Z)=Hφ(X)。
如果是连续型分布,由于qφ(x|z)=δ(x-G(z))是一个确定性的模型,也可以理解为均值为 G(z) 、方差为0的高斯分布N(x;Gφ(z),0)。我们将其推广到常数方差的情况![]() ,代入计算发现是Hφ(X|Z)的值是一个常数
,代入计算发现是Hφ(X|Z)的值是一个常数![]() ,然后取 σ→0,不过发现结果是无穷大。无穷大原则上是不能计算的,但事实上方差也不需要等于 0,只要足够小,肉眼难以分辨即可。此时
,然后取 σ→0,不过发现结果是无穷大。无穷大原则上是不能计算的,但事实上方差也不需要等于 0,只要足够小,肉眼难以分辨即可。此时![]() 依然是一个常数。
依然是一个常数。
所以,总的来说我们可以确定互信息 Iφ(X,Z) 与熵 Hφ(X) 只相差一个无关紧要的常数,所以Hφ(X) 可以被替换为 Iφ(X,Z)。
现在回到第三节最后我们得到的训练表达式:
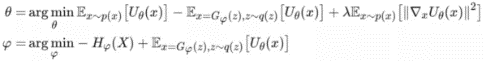
将Hφ(X) 替换为 Iφ(X,Z),得到:

现在我们要最小化 −Iφ(X,Z) ,也就是最大化互信息 Iφ(X,Z)。
互信息估计的方法有两种,如果需要精确估计互信息的话,可以采用通过 f 散度的方式估计,由于这种方法太复杂,感兴趣的读者可以参阅苏剑林老师的另外一篇文章:https://kexue.fm/archives/6024;下面介绍另外一种不那么精确的方法,就是通过互信息下界的方式估计。
我们回顾一下互信息的定义:
![]()
记 qφ(z|x)=qφ(x|z)q(z)/qφ(x),这代表精确的后验分布;然后对于任意近似的后验分布 p(z|x),我们有:

也就是说,互信息大于等于∬qφ(x|z)q(z)logp(z|x) 加上一个常数。如果最大化互信息,可以考虑最大化这个下界。由于 p(z|x) 是任意的,可以简单假设![]() ,其中 E(x) 是一个带参数的编码器,代入计算并省去多余的常数,可以发现相当于在生成器加入一项 loss:
,其中 E(x) 是一个带参数的编码器,代入计算并省去多余的常数,可以发现相当于在生成器加入一项 loss:
![]()
所以,基于互信息下界估计的思路,最终的训练表达式就变成了:

综上,我们在本节实现了 Hφ(X) 的处理和求解,从而完成了整个 GAN 和能量模型的推导。
评 论
